·收藏本站
关注试商方法,提升数学素养 ——浅谈珠心算除法10种试商方法
2019/8/15 13:17:34 网站:http://www.shzxs.org 来源:上海市珠算心算协会
关注试商方法,提升数学素养
——浅谈珠心算除法10种试商方法
杨 岚 王亚宁
【内容摘要】
多位数笔算除法教学的关键是试商,同理,珠心算除法的关键也在于试商。大多数学生初次接触珠心算除法时,就被“试商”吓倒了。商不是偏大就是偏小,反反复复商了又改、改了再商,影响了除法的准确性和速度,浪费了大量的时间,为此,多年来我注重珠心算除法试商教学,大胆尝试了珠心算除法“试商”规律,积累试商方法和技巧。
【关 键 词】珠心算 除法 试商技巧 规律方法
【正 文】
多年的教学经验告诉我们:只有提高珠心算除法试商的准确性,才能提高学生珠心算除法的计算能力;只有熟练掌握一位数除法试商方法,才能让学生提高多位数除法试商的技能,而一位数珠心算除法试商的关键在于熟记“大九九”乘法口诀和快速完成“单积一口清”。
珠心算除法与笔算除法的运算顺序、试商方法、计算步骤完全相同,分为五步:试商→置商→减积→落余→续除,可见,试商是珠心算除法的关键,是珠心算除法教学的重点和难点。为了突破这一难点,提高学生试商技能,教学中,我特别注重引导学生“观察例题特点→分析试商规律→总结试商方法→准确快速试商→使学生试商达到灵活、准确、快速。”下面我将自己多年潜心钻研、实践、积累、总结出来的10种试商方法和技巧分享给大家。
一、“口诀”试商法。
用“乘法口诀求商”是现行北师大小学数学二年级上册第四、八单元的关键。教材采用的是“小九九”乘法口诀求商。理由是“小九九”乘法口诀少,易记忆,减轻学生记忆负担,可是运用“小九九”乘法口诀试商却具有一定的局限性,因此教学时我将“小九九”乘法口诀改为“大九九”乘法口诀,提高了除法试商的速度和准确性。“大九九”乘法口诀是乘除法计算的重要工具,试商时,先看除数是几,就用几的“大九九”乘法口诀快速试商,下面我分两类进行教学:
第一类: 42÷7= 36÷9= 48÷8= 56÷8= 15÷5=
第二类: 42÷6= 36÷4= 48÷6= 56÷7= 15÷3=
第一类题型试商教学:
42÷7=?先看除数是7,就用7的乘法口诀来试商,想:□个7是42(六七42),直接商6,即42÷7=6。
36÷9=?方法同上,先看除数是9,就用9的乘法口诀来求商,想:几个9是36(四九36),直接商4,即36÷9=4。
例1:42÷2=21
1、动手分一分,理解算理。
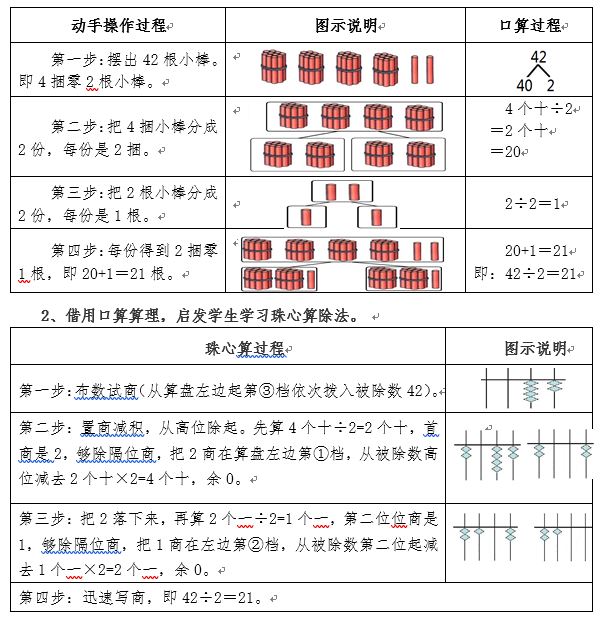
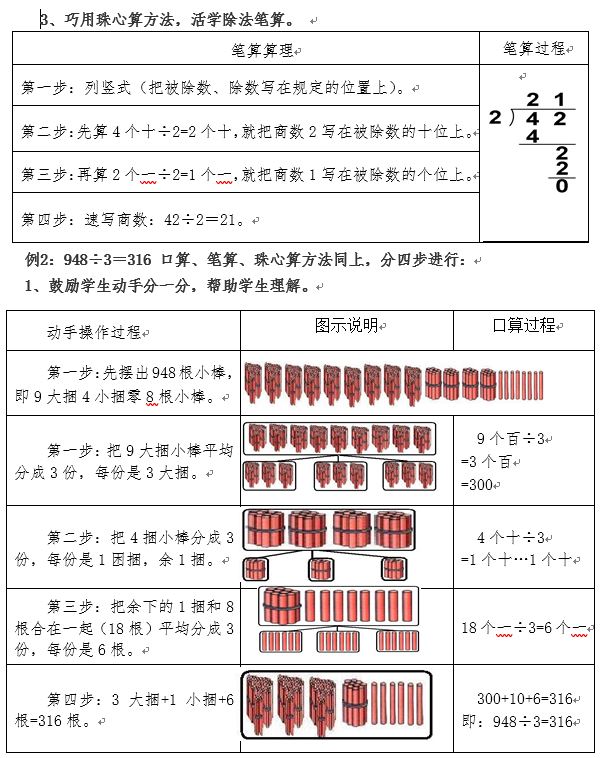

二、“四舍”试商法。
“四舍”试商法是指除数个位上的数字是1、2、3、4时,在一般情况下,可以把除数的尾数直接舍去,把它看作与除数接近的整十数来试商。用“四舍”试商法来试商,除数看小了,初商易偏大,要将初商调小,调商方法是:“初商减1”。理由是:除数若看小,初商容易大,调商速减1。
例1:147÷21,运用“四舍”试商法将除数21看作20,用2的口诀来试商,想口诀:□×2=14,确定147÷21的初商为7,再用一口清得出7×21=147,即147÷21的商为7正合适。
例2:581÷83,运用“四舍”试商法将除数83看作80,用8的口诀来试商,想口诀:□×8=56<58,确定581÷83的初商为7,再用一口清验证:7×83=581,得出581÷83的商为7正合适。
例3:如43O÷62,运用“四舍”试商法把除数62看作60,用6的口诀来试商7,7×62=434,积比被除数大,说明商7偏大了,应改为6,6×62=372,43O-372=58,58比除数62小,说明商6合适。
“四舍”试商法,把除数看小了,初商偏大,要把初商进行调整,调商方法是:“初商减1”。“四舍”试商法试商规律是:少看少商1,即除数看小了,商易变大,调商速减1 。
三、“五入”试商法。
“五入”试商法是指当除数个位上的数字是5、6、7、8、9时,在一般情况下,可将除数看作与其接近的整十数来试商。用“五入法”试商,商容易小,因为试商时把除数首位多看1,用“五入法”试商,初商易小,必将初商调大,调商方法是“初商加1”。
例1:850÷17=□,把17看作20,用2的口诀来试商,从高位除起,8里面有4个2,把17看成20,多看商多1(4+1=5),试商为5,再用单积“一口清”5×17=85一次确定商为5,正好合适,即850÷17=5。
例2:152÷38=□,把38看作40,用4的口诀来试商,15里面有3个4,把38看成40,多看多商1(3+1=4),试商为4,再用单积“一口清”4×38=152一次确定商为4,正好合适,即152÷38=4。
例3:261÷29=□,把29看作30,用3的口诀来试商,26里面有8个3,把29看成30,多看多商1(8+1=9),试商为9,再用单积“一口清”9×29=261一次确定商为9正好合适,即850÷17=5。
又如278÷38,把除数“五入”看作40,试商6,6×38=228,278-228=50,余数20比除数38大,说明商偏小了,改商为7,7×38=266,278-266=12,余数12比除数38小,商7合适。从这道题看出,把除数往大看,初商容易小。因此要记住“五入商易小,初商可加1”的规律。
用“五入法”试商,将除数看大,初商易小,必将商调大,调商方法是“初商加1”,规律是“多看多商1”。
四、口算试商法。
“口算试商法”适用于除数是两位数的除法。当除数的个位上的数是4、5、6时,可将除数看作□5(几十五)来试商,直接商5。北师大小学数学四年级上册教材85页例题:156÷26=□,如果用“五入法”把26看作30来试商,商5偏小,因为5×26=130,156-130=26,余26,而26里面还有1个26,将初商5改为6,调商几次,非常麻烦,如果把26看成25,口算“6×25=150”,可直接商为6,可见:将除数是□4、□5、□6,看成□5试商方便快速,这就是我们所提倡的“口算试商法”。
采用“口算试商法”首先要加强一位数乘几十五的训练,只要学生能脱口而出□×□5的积,用“口算试商法”就很容易。在教学中,我常常把除数是14、15、16看作15来试商;把除数24、25、26看作25来试商……这样试商又准又快。如80 ÷16=□,快速口算便知:5×16=80,直接试商5(80÷16=5);240÷25=□,快速口算便知:9×25=225,直接试商9(240÷25=9),这种试商法简称“够半商5”。又如:270÷54=□,快速口算便知:5×54=270,直接试商9。
“口算试商法”要重视乘法的口算训练,学生只要对一些特殊数的乘积强化熟练,采用“口算试商法”感到游刃有余,简单简便,准确性高。
五、“倍数”试商法。
“倍数试商法”是指当被除数是除数的倍数时,就不必要用“四舍五入”法来试商,直接用他们之间的倍数关系试商就可以了。如:168÷42 ,这道题被除数的前两位数字是16,而除数的首位数字是4,而16是4的4倍,直接商4,用一口清速算,得4×42=168,168-168=0,余0,商4正好合适。当被除数的首位数字是除数首位数字的倍数时,就用“倍数试商法”直接试商。分三种情况:
1、当被除数的前两(三)位数字正好是除数的一半(或接近于一半)时,就商5。如:234÷42的被除数的前两位23比除数42的一半21稍大,商5合适;495÷93的被除数的前两位49比除数93的一半46稍大,商5合适;1945÷388的被除数的前两位19比除数38的一半大,商5合适。
2、当被除数的前两(三)位数字小于除数的一半时,商4、3合适。如:148÷36的被除数的前两位14比除数36的一半18小,商4较合适;2184÷526的被除数的前两位21比除数52的一半26小,试商4合适。
3、当被除数的前两(三)位数字大于除数的一半时,商6、7合适。如:505÷72的被除数的前两位50比除数72的一半大一些,商7合适。 1238÷198的被除数的前两位数字12比除数19的一半大一些,商6合适。“倍数试商法”使用起来非常简便,利于提高试商的正确性和速度。
六、“首位”试商法。
“首位试商法”是从被除数与除数的首位数字关系分析试商,分为两种情况:
第1种情况是被除数的首位数够除除数的首位数,直接试商。如:864÷54,被除数和除数的的首位数字分别是“8”和“5”,用首位试商法:8里面有1个5,首商为1,用一口清验证(86-1×54),余32;把4落下来,接着继续除324÷54,被除数的前两位数字是“32”,除数的首位数字是“5”,想:□×5=3□,又比32小,直接商6,再用一口清验证(6×54=324),324-324=0,余0,。采用“首位试商法”能达到快速算出864÷54=16。
第2种情况是被除数的前两位数不够除除数的首位数,这时就从被除数与除数的首位数的关系进行分析初商。如:3591÷57,被除数和除数的首位数字分别是“3”和“5”,3﹤5,不够除,就看被除数的前两位数字“35”和除数首位数字“5”之间的关系进行试商,“35”里面有7个”5”,商7,再用一口清验证(7×57=399),399﹥359,偏大,改7为6,再用一口清验证:6×57=342, 359-342=17,余17;把1落下来,171÷57,17里面有3个5,试商3,用一口清验证:7×57=171,171-171=0,得出3591÷57=63。
“首位试商法”的特点是:不用考虑除数个位数字的大小,初商可能偏大,个位数字越大,与初商相乘的积越大,初商应调小,调商时灵活调商即可。
七、 “同头”商9、8 法。
“同头商9、8法”是指被除数与除数的首位相同(即“同头”),试商分两种情况:1、当被除数和除数的最高位相同,而第二位的差数不超过首位时,通常可以商“9”,如440÷46、802÷83、900÷98等。2、当被除数和除数的最高位相同,而第二位的差数超过首位时,通常可以商“8”,如410÷46、152÷18、325÷38等。
知道了“同头”商9、8 的规律,还要在计算中慢慢体会如何正确应用,不断积累经验,增强试商的准确性,提高试商的速度。
首位数字是“1”时,利用“同头试商9、8法”是有规律的,要先看被除数与除数的前一(两)位数是否相同;再看次位数字相差几;最后根据同头试商的规律进行试商,这样试商简便、迅速,在教学中,我常常用同头无除商9、8 这一规律,方便多了。
八、“同舍同进”试商法。
“同舍同进”试商法是指把被除数和除数的次位数字同时舍去或同时向前进1,然后再试除。如112÷28用“同进法”试商比较简便。除数28≈30,被除数112≈120,用3的口诀来试商,想4×3=12,试商4,用一口清验证:4×28=112, 112÷28=4刚合适;用“同舍法”试商,除数28≈20,被除数112≈100,用2的口诀试商,想5×2=10,把除数28看作20,用“少看少商1”的(5-1=4)规律试商4,用一口清验证:4×28=112,即112÷28=4刚合适。又如:126÷21用“同舍法”试商较简便。把除数21≈20,被除数126≈120,用2的口诀试商,想6×2=12,试商6,用一口清验证:6×21=126,商6正好合适。“同舍同进法试商”,虽之除数和被除数有变化,但试商一次成功率高。
九、“折半”试商法。
“折半试商法”是指被除数的前一(两)位数字正好是除数前一(两)位数的一半或接近一半时,试商4、5正合适。
例1:490÷98=□,被除数的前两位49,刚好是除数98的一半,直接商5,用一口清验证:5×98=490,余0,商5正合适。
例2:330÷68=□,被除数的前两位33接近除数68的一半34,而又小于34,所以不能直接商5,商4,用一口清验证:4×68=272,330-272,余58,而58<68,商4合适。
例3:350÷68=□,被除数的前两位35接近除数68的一半34,且大于34,所以直接商5,用一口清验证:350-5×68=340,余10,10<68,商合适。
用“折半”试商法,只看被除数和除数前一(前)两位,只要被除数接近除数的一半,商4、5最快速。
十、“差数”试商法。
“差数”试商法是指除数是十几时。当除数是11-19之间的自然数,并且被除数的前两位不够除时,按照除数与被除数前两位的差来试商比较方便。其规律分为以下四种情况:
1、差1差2试商9,个别下调改商8。如:156÷16,次位数字5和6相差1,商9合适;112÷12,11与12相差1,试商为9,用一口清验证:9×12=108,112-108=4<12,商9刚合适;112÷13,11与13相差2,试商9偏大,改为8,用一口清验证:8×13=104,113-104=9<13,商8刚合适。其试商规律是:“差1差2试商9,个别下调改商8”。
2、差3差4试商8,个别下调改商7。例如:160÷19,16和19相差3,试商8,用一口清验证:8×19=152,152<160,商8刚合适。150÷19,15和19相差为4,试商8,用一口清验证:8×19=152,152>150,商8偏大,改为7 刚合适。其试商规律是:“差3差4试商8,个别下调改商7”。
3、差7差8试商6,个别下调试商5。如:144÷19,次位数字4和9相差5,商7刚合适;102÷17,次位数字0和7相差7,商6刚合适;通过观察分析,总结如下:“差5差6试商7,个别下调试商6”;“差7差8试商6,个别下调试商5”。“差数试商法”,规律性强,易学易懂,试商次数少,速度快,正确率高。
总之,在珠心算除法教学时,学生只有认真观察除数和被除数之间的关系,通过认真分析,反复练习,试商速度逐渐增快,这样学生就能把课本知识逐步融会贯通,灵活选择最佳试商方法,提高试商的准确性和试商效率。可是,学生全部掌握这些试商方法是有一定的难度,因此不管用那种方法试商,只要学生具备扎实的口算基本功和善于观察数与数之间的关系、特点,灵活应用,才会巩固除法试商的技巧,才能不断提高试商的速度和计算的正确率。