上海市珠算心算协会

您现在的位置：网站首页>详细信息

《九章算术》刘徽注中的率以及率思想方法的现代运用

2019/5/29 9:31:19 http://www.shzxs.org 来源：上海市珠算心算协会阅读：4596人次

《九章算术》刘徽注中的率以及率思想方法的现代运用

刘芹英

《九章算术》是中国古代数学的代表著，有狭义、广义两种，广义的《九章算术》包括《九章算术》本文、魏刘徽注、唐李淳风注。率是中国古代数学优秀思想方法，必然在《九章算术》中占据重要位置。了解率在《九章算术》中的论述及运用情况，对于认识、理解、研究率思想方法的现代开发和运用有着重要意义。

一、《九章算术》本文中的率

（一）《九章算术》本文中“率”字出现的次数统计

在《九章算术》本文中多次出现“率”字，但没有人做过统计。经本人统计，率字在《九章算术》本文中共出现65次。其中，在卷一方田章中，率字只出现一次；而在卷二粟米章中，率字共出现了24次，主要出现在粟率、经率、其率和反其率等问题中；占本文中率字出现总次数的1/3还多。卷三衰分章中出现3次，卷四少广、卷五商功和卷八方程章中均没有出现率字，卷六均输章中率字出现了3次；卷七盈不足章中率字出现10次，卷九勾股章中率字出现了25次。

（二）《九章算术》本文率的运用

虽然《九章算术》本文中率的应用在算术、代数、几何等方面均有涉及。如在算术与代数方面主要有今有术、盈不足术、齐同原理等，在几何方面如勾股章等。但在《九章算术》本文中，论述、运用率最具代表性的是卷二“粟米”章和卷九勾股章。

卷二粟米章中论述了今有术、经率、其率和反其率。 “今有术曰：以所有数乘所求率为实，以所有率为法，实如法而一。”按照这句话的意思，我们可以写出如下

所有数×所求率

公式：所求数 = ———————— 所有率

“经率术曰：以所买率为法，所出钱数为实，实如法得一钱。”用现在的公式表示出来就是：一（单位）钱数= 所出钱数 / 所买率；

“经率术曰：以所求率乘钱数为实，以所买率为法，，实如法得一。”用现在的公式表示就是：所求数= 所求率×钱数/ 所买率

“其率术曰：各置所买石、钧、斤、两以为法，以所率乘钱数为实，实如法而一。不满法者，反以实减法，法贱实贵。” 用现在的公式表示出来就是：

所求价钱（价格） = 所率×钱数/ 买物重量

“反其率术曰：以钱数为法，所率为实，实如法而一。不满法者，反以实减法，法少实多，二物各以所得多少之数乘法实，即物数。” 用现在的公式表示出来就是：物数= 所率/ 钱数

卷三中出现的三个率字出现在一道题目的术曰中“今有甲持粟三升，乙持糲米三升，丙持糲饭三升，欲令合而分之，问各几何？答曰：甲二升一十分升之七；乙四升一十分之五；丙一升一十分之八。术曰：以粟率五十、糲米率三十、糲饭率七十五为衰，而反返衰之副并为法，以九升乘未并者，各自为实，实如法得一升。”

卷七盈不足章中，论述了盈不足、两盈两不足、盈适足不足适足等术。

“盈不足术曰：盈不足相与同共买物者，置所出率盈不足各居其下。令维乘所出率，并，以为实。并盈、不足为法。副置所出率，以少减多，余，以约法实。实为物价，法为人数。”

“其一术曰：并盈、不足为实。以所出率，以少减多，余为法。实如法得一人。以所出率乘之，减盈、增不足，即物数。”

“两盈、两不足术曰：两盈、两不足相与同共买物者。置所出率，盈、不足各居其下。令维乘所出率，以少减多，余为实。两盈、两不足，以少减多，余为法。实如法而一。有分者，通之。副置所出率，以少减多，余，以约法、实。实为物价，法为人数。”

“其一术曰：置所出率，以少减多，余为法。两盈、两不足，以少减多，余为实。实如法而一，得人数。以所出率乘之，减盈、增不足即物价。”

“盈适足、不足适足术曰：以盈及不足之数为实。置所出率，以少减多，余为法。实如法得一人。其求物价者，以适足乘人数，得物价。

卷九勾股章中，在五个算题后面的一段话中首先出现率。“此四雀一燕语一雀五燕衡适平，并重一斤，故各八两，列两行程数左行头位其数是一可省乘，令右行徧乘左行，而取其法实于左右行数，多以右行取其数，左头位减尽，中法下实，即每枚当重，宜可知也。按此四雀一燕与一雀五燕其重等，是三雀四燕重相当，雀率重四，燕率重三也。诸再乘之率，皆可异术求之，即其数也。”后面还出现“通率”、“其率”、“行率” 等用法。

“今有二人同所立。甲行率七，乙行率三。乙东行。甲南行十步而邪东北与乙会。问甲、乙行各几何？答曰：乙东行十步半；甲邪行十四步半及之。术曰：令七自乘，三亦自乘，并而半之，以为甲邪行率。邪行率减于七自乘，余为南行率。以三乘七为东行率。置南行十步，以甲邪行率乘之。副置十步，以乙东行率乘之，各自为实。实如南行率而一，各得行数。”

由上可以看出，在《九章算术》本文中，率字出现的次数并不是太多，而且有三章中根本就没有出现率字。

二、《九章算术》刘徽注中的率、论述和运用

刘徽注是目前留存下来最早的、保存最为完整，而且也是最重要的《九章算术》注释。刘徽注释是在其深入研究《九章算术》数理的基础上，结合其搜集到的前代和同时代学者们的九章算术研究心得，完成了杰作《九章算术注》。刘徽把率的应用拓展到《九章算术》的大部分术文和约200百个题目解法中，这也说明了率在刘徽注中的重要性。

（一）《九章算术》刘徽注中“率”字出现的次数统计

在《九章算术》本文中，虽然只有65处出现并使用了率，而刘徽则把率看成是运算的纲纪，将率的应用拓展到大部分算法的论证和200个左右的题目的解法中。据本人统计在《九章算术》刘徽注中率字共出现423次。其中，在卷一方田章刘徽注中率字出现27次：卷二粟米章刘徽注中率字出现85次；卷三刘徽注中率字出现36次；卷四刘徽注中率字出现26次；卷五刘徽注中率字出现38次；卷六刘徽注中率字出现112次；卷七刘徽注中率字出现12次；卷八刘徽注中率字出现40次；卷九勾股章刘徽注中率字出现47次。

可以看出，在《九章算术》刘徽注中，率字出现的次数比本文中要多得多，是本文中的6.5倍。

（二）《九章算术》刘徽注中率的论述

在《九章算术》刘徽注中，率字出现的次数如此多，说明了率的重要性。下面从率定义和性质等方面来阐释刘徽注中有关率的论述。

1、率的定义

在《九章算术》卷一“方田”章的经份术的注释中，刘徽以其高超的概括能力给出下面率的定义：“凡数相与者谓之率。”

刘徽所给出的“率”的定义，反映了相关事物之间的数量关系的本质属性，并且与先秦以来关于率的约定俗成的含义一致。

关于如何求出诸量之间的率，刘徽明确给出了：“少者多之始，一者数之母。故为率者必等之于一。据粟率五、粝率三，是粟五而为一，粝米三而为一也。欲化粟为米者，粟当先本是一。一者，谓以五约之，令五而为一也。讫，乃以三乘之，令一而为三。如是，则率至于一，以五为三矣。”如果用现代汉语来解释这段话，就是是告诉人们，要想求出诸物之间的率，必须先确定“单位”（一）；而且刘徽把“一”作为“数之母”。

在卷一“经分术曰”的注释中，刘徽不仅给出了相与率的概念，紧接着就给出了相与率的求法：“率者，自相与通，有分则可散，分重叠则约也。等除法实，相与率也。”用现代话来说，就是相与率要求诸量之间是互素关系，如果诸量之间有大于1的公约数，就要用公约数去除诸数，直至成为互素关系为止。

按照刘徽对率的定义，分数的分子与分母可以看成率关系，因分数的分子与分母之间也是相与关系。而且刘徽的这一理论与现代算术理论中关于最简分数的定义完全一致。

2、率的性质

刘徽在卷三衰分章的倒数第4个题目：“今有生丝三十斤，干之耗三斤十二两。今有干丝一十二斤。问生丝几何？术曰：置生丝两数除耗数，余，以为法，三十斤乘干丝两数为实。实如法得生丝数。”的注释中给出率如下性质：

“凡所得率知，细则俱细，粗则俱粗，两数相抱而已。”其意思是：构成同一率关系的诸量同时扩大或者缩小不为零的相同倍数，其率关系保持不变。

按照刘徽对率的定义，分数是分子、分母的率关系。由率得定义和性质，刘徽在卷一方田章合分术注中给出了分数运算的三种等量变换。刘徽注释中讲到：“方以类聚，物以群分。数同类者无远，数异类者无近。远而通体知，虽异位而相从也；近而疏形知，虽同列而相违也。然则齐同之术要矣，错综度数，动则斯谐，其犹佩觿解结，无往而不理焉。乘以散之，约以聚之，齐同以通之，此其算之纲纪乎。”刘徽在上述注释中，明确给出了分数运算的三种等量变换：“乘以散之，约以聚之，齐同以通之。”；同时也阐明了等量变换在数学运算中的重要性，更说明了率是算法之纲纪。

（三）《九章算术》刘徽注中率的应用术文举例

《九章算术》刘徽注中，率不仅应用在算术、代数方面，还应用在几何方面，下面就率在算术、代数、几何等方面的代表性应用术文举例说明。

1、刘徽注中率在算术方面的应用术文举例

率在算术问题中的应用最多，也最为广泛。限于篇幅，我们这里只以今有术和齐同术举例。

《九章算术》中今有术的原文在前面已经讲到，这里不再赘述。虽然今有术在《九章算术》本文中的应用仅限于粟米章中三十一个各种谷物互换问题，但刘徽称其为“都术”，即普遍方法。“此都术也。凡九数以为篇名，可以广施诸率，所谓告往而知来，举一隅而以三隅反者也。诚能分诡数之纷杂，通彼此之否塞，因物成率，审辨名分，平其偏颇，齐其参差，则终无不归于此术也。”

刘徽注释今有术的应用进行了拓展，将《九章算术》的许多术文都归结为今有术，使今有术的应用遍布几乎每一章。经率术显然归于今有术；衰分术是比例分配的方法，刘徽在论证衰分术正确性的基础上，将衰分术归结到今有术；同样，将均输术也归结为今有术；他还将许多别的算术问题都归结到今有术。如：犬追兔问题、客去忘衣问题、复比例问题、归一问题、还原问题、连锁比例问题等都归结为今有术来进行处理和解答。

今有术曰：以所有数乘所求率为实，以所有率为法，少者多之始，一者数之母，故为率者必等之于一。据粟率五，粝率三，是粟五而为一，粝三而为一也。欲化粟为粝米者，粟当先本是一。一者谓五约之，令五而为一也。讫，乃以三乘之，令一而为三。如是，则率等于一，以五为三矣。然先除后乘或有余分，故术反之。又完言之，知粟五升为粝米三升。分言之，知粟一斗为粝米五分斗之三。以五为母，三为子。以粟求粝米者，以子乘，其母报除也。然者所求之率常为母也。臣淳风等谨按：宜云“所求之率常为子，所有之率常为母”。今乃云“所求之率常为母”，知脱错也。实如法而一。

显然，原文比较简单：“今有术曰：以所有数乘所求率为实，以所有率为法，实如法而一。”就这么一句。但通过刘徽作注释，就大大的丰富了。

今有兔先走100步，犬追之二百五十步，不及三十步而止。问犬不止，复行几何步及之？

术曰：置兔先走一百步，以犬走不及三十步减之，余为法。以不及三十步乘犬追步数，为实。实如法得一步。

刘徽认为：“此术以不及三十步减先走一百步，余七十步，为兔先走率。犬行二百五十步为追及率。约之，先走率得七，追及率得二十五。于今有术，不及三十位所有数，二十五为所求率，七位所有率，而今有之，即得也。”

齐同术：齐同术源于分数加减法。如刘徽在合分术中所说：“众分错杂，非细不会，乘而散之，所以通之，通之则可并也。”这段话实际上包含括两步运算：第一步首先使诸分数的分母同一；第二步是使个分数的分数值保持不变。前者是同，同其母；后者是齐，齐其子，这就是齐同术。刘徽对齐同术的论述：“凡母互乘子谓之齐。群母相乘谓之同。同者，相与通同共一母也；齐者，子与母齐，势不可失本数也。”刘徽还提出了另一种齐的方式方法：“其一术者，可令母除为率，率乘子为齐。”上述两种齐同方法，都没有求诸分母的最小公倍数，以其为分母，而是以诸分母的连乘积为公分母，完成加减法之后再约分，化成最简分数。

齐同术不仅用于与率或今有术有关的方法和问题上，而且还可以用于其它方法和问题。如均输章的第20问：今有凫起南海，七日至北海，雁起北海，九日至南海。今凫雁俱起，问何日相逢？术曰：并日数为法，日数相乘谓为实，实如法得一日。而刘徽则是采用齐同原理解答：“此术置凫七日一至，雁九日一至。齐其至，同其日，定六十三日凫九至，雁七至。今凫、雁俱起而问相逢者，是为共至。并齐以除同，记得相逢日。故并日数为法者，并齐之意；日数相乘为实者，犹以同位实也。”上述方法刘徽采用的是“齐其至，同其日”的方法，他认为也可采取同距离之分，齐其日速的方法实现齐同：“一日：凫飞日行七分之一，雁飞日行九分之一。齐而同之，凫飞定日行六十三分至之九，雁飞定日行六十三分至之七，是为南北海相去六十三分，凫日行九分，雁日行七分也。并凫、雁一日所行，以除南北相去，而得相逢日也。”

刘徽还应用齐同原理处理盈不足问题。他把不足称为朒，把所出率称为假令。他说：“盈维乘两设者，欲为同齐之意。举共买物，人出把，盈三；人出七，不足四。齐其假令，同其盈、朒。盈、朒俱十二，通计齐则不盈不朒之正数，故可并之为实，并盈、不足为法。齐之三十二者，是四假令，有盈十二；齐之二十一者，是三假令，亦朒十二。并七假令合为一实，故并三、四为法。注云若两设有分者，齐其子，同其母。此问两设俱见零分，故齐其子，同其母。又云令下维乘上。讫，以同约之。不可约，故以乘，同之。所出率以少减多者，余，谓之设差，以为少设，则并盈、朒，以为定实。故以少设约定实，则法为人数，适足之实为物价。盈、朒当与少设相通。不可遍约，亦当分母乘设差，为约法、实。”刘徽在这段注释中，不仅给出假令为整数情形的齐同过程，也给出了两假令都是分数情形的齐同过程。

2、刘徽注中率在代数方面的应用术文举例

率在代数方面的应用主要体现在方程术中，体现在方程的定义、方程直除法、互乘相消法和方程新术等几个方面。

方程定义：刘徽的方程定义：“程，课程也。群物总杂，各列有数，总言其实。令每行为率，二物者再程，三物者散程，皆如物数程之，并列为行，故谓之方程。行之左右，无所同存且为有所据而言耳，此都术也。”刘徽的定义与方程的本义是一致的，而且定义中“令每行为率”这句话至关重要，相当于把方程的每一行都看成一个整体，看成相对于其它行的率，与现代方程理论中的行向量有相似之处。

同解变换：正是由于刘徽在方程的定义中，令每行为率，使得在方程问题的处理中，就可以施行率的三种等量变换：一是对某一行，可以施行“乘以散之” ，即对一行的各项同时扩大同一倍数不影响方程得解；二是对某一行，可以施行“约以聚之” ，即对一行的各项同时缩小同一倍数不影响方程得解；三是对两行，可以施行“齐同以通之”，即使两行中某对应的项相同，而使其余的项分别与该项相齐，不影响方程的解。也就是说，刘徽将率的三种等量变换转换成了方程消元法中得到的同解变换。在直除消元法中，上述变换时通过两行直除得到的。刘徽注中讲到：“先令右行上禾乘中行，为齐同之意。为齐同者，谓中行直减右行也。从简易虽不言齐同，以齐同之意观之，其义然矣。”

正负术：刘徽在方程章中给出了正负数的定义：“令两算得失相反，要令正负以名之。”这个定义说明了，正负是相对而言的，是相互依存的。刘徽认为，方程理论完全适用于负系数方程。“方程自有赤黑相取，法实数相推求之术，而其并减之势不得广通，故使赤黑相消夺之。”而且对含有负系数的方程，仅一步说道：“赤、黑相杂足以定上下之程，减、益虽殊足以通左右之数，差、实虽分足以应同异之率。然则其正无入者入以负之，负无入以正之，其率不妄也。”

互乘相消法：由于直除法消元要反复相减，比较繁琐。刘徽在《九章算术》章题目：今有牛五、羊二，直金十两；牛二、羊五，直金八两。问牛、羊各直金几何？的注释中创造了“互乘相消法”。原术文只有三个字“如方程”，刘徽注释曰：“假令威同齐，头位为牛，当相乘。右行定，更置牛十、羊四，直金二十两；左行牛十、羊二十五，直金四十两。牛数等同，金多二十两者，羊差二十一使之然也。以少行减多行，则牛数尽，惟羊与直金之数见，可得而知也。以小推大，虽四、五行不异也。”这就是互乘相消法，用该方法一下子就实现了齐同，比直除相消法简便很多。而且，刘徽认为互乘相消法是普遍方法，对任意多行的方程都适用。

方程新术：由刘徽给出的方程定义可知：方程各行就是诸物之率的线性关系。他创造的方程新术，最后都归结到了“今有术”。刘徽注曰：“方程新术曰：以正负术入之。令左、右相减，先去下实，又转去物位，则其求一行二物正、负相借者，是其相当之率。又令二物与他行互相去取，转其二物相借之数，即相当之率也。各据二物相当之率，对易其数，即各当之率也。更置成行及其下实，各以其物本率今有之，求其所同，并，以为法。其当相并而行中正负杂者，同名相从，异名相消，余以为法。以下置为实。实如法，即合所问也。一物各以本率今有之，即皆合所问也。率不通者，齐之。”

“其一术曰：置群物通率为列衰。更置成行群物之数，各以其率乘之，并，以为法。其当相并而行中正负杂者，同名相从，异名相消，余为法。以成行下实乘列衰，各自为实。实如法而一，即得。”

3、刘徽注中率在几何方面的应用术文举例

《九章算术》中率在几何方面的应用仅限于勾股数组公式。而刘徽则把率的应用扩展到圆周率、面积、体积、勾股容方、容圆、一次测望、重差等问题和解法中。限于篇幅，这里不多再多说。

三、率思想方法的现代开发及研究运用

率早在《九章算术》刘徽注中就给出了明确的定义，并得到广泛的应用。但在中国数学教育全盘西化后丢掉了。其实，这是不该丢的，率在现代数学教育中不仅有用武之地，而且有独到的作用。下面从四个方面简要谈谈率的现代应用。

（一）从解应用题中发现“量-单位-数相互联系分析法”——率思想方法

20世纪五、六十年代，郭启庶教授在其从事的小学数学教学中遇到了应用题这个“老大难”问题，他在对该问题解决方法的思考、研究过程中，受华罗庚先生文章《大哉数学之为用》的启发，该文开头讲说道：“数（sh\u）起源于数（sh∨u）,如一、二、三、四、五……，一个、两个、三个……。量（lia\ng）起源于量（lia/ng），先取一个单位作标准，然后一个单位一个单位地量。天下虽有各种不同的量（各种不同的量的单位如尺、斤、斗、秒、伏特、欧姆和卡路里等等），但都必须通过数才能确切地把实际情况表达出来。所以‘数’是各种各样不同量的共性，必须通过它才能比较量的多寡，才能说明量的变化。” 郭启庶教授在仔细思考、认真琢磨这段话的基础上，最后将其归结为“量-单位-数及其相互联系”，认为这是解应用题的基本要素。并由此自创了解答应用题的方法：“量-单位-数及其联系”分析法——表解法，写了《解应用题的桥和路》一书（因文革缘，此书在1982年才得以出版）。当时，他并不知道“量-单位-数及其联系”就是中国古代数学中早已存在的——率思想方法；后来，他在学习和研究中国古代数学史时，特别是研读郭书春先生《九章算术》研究方面的著作时，才发现“表解法”原来就是中国古代数学所特有的优秀思想方法——率的运用。郭启庶教授认为率是一种思想方法，为了明确和统一，本文从现在开始就不单说“率”，而是说“率思想方法”。对中国古代数学优秀思想方法——率思想方法，现代不少人了解不多，其主要原因是由于中国数学教育全盘西化后，中国古代数学中的很多优秀思想方法被完全丢掉了的缘故。由于中国古代数学运用率的传统被中断，造成现代学者花了很多长时间、付出了很多努力、搭上许多倍的功夫，才又回到“重新发现”和研究运用刘徽早已发现了的中国优秀的数学思想方法——率思想方法。

率思想方法的通俗描述和解释为：率思想方法就是在用数刻划量和用数学解决实际问题的过程中，关于量、计量单位、数之间的联系和相互作用的思想方法。率思想方法不只用于解应用题，其实在现代基础数学教育的各个方面都有其重要作用和意义。从数学启蒙教育开始，率思想方法不仅对于解决数学从哪里发端？如何生长？及其数学发展的规律性问题等方面有决定性意义，而且在认识数学、运用数学、论证数学等方面都有巨大的简化作用。

（二）创立率的范式（率范或率表），使率的运用更简明易懂

在现代基础数学教育中，为了使率思想方法更简捷易懂，能够更广泛地被人们所接受和运用，就必须改善其表达形式或表述方式。首先，应当明确有关的概念和关系：如量、单位（计量单位）、用数来刻划量、数量关系等，还有如华罗庚先生所指出的“‘数’是各种各样不同量的共性，必须通过它才能比较量的多寡，才能说明量的变化。”即首先用数来刻划量，以便精确表达量的大小、量的变化和对现实事物的量进行数学处理（运算、推理，包括运用电子计算机处理）。

郭启庶教授根据其几十年来的数学教学经验，加上孜孜不倦的探索，从数学基本要素率（“量-单位-数及其相互关系”）入手，经过分析研究，最终给出率思想方法的范式（简称率范），即“量-单位-数对应表”（或说率表）。

率表是“位值制”（运用空间因素）思想的拓展，运用空间观念帮助理解运算意义、数量关系、组织算式、解答应用题，等等。在实际数学教学中，让学生明确有关概念，运用率范（率表）和四角阵原理，不仅可以轻松解决应用题，更重要的是对数学教学有巨大的简化作用。下面用两个例子来简要说明其简化作用。

例1. 《九章算术》卷二“粟米”第二十题：

今有粝米十五斗五升五分升之二，欲为粟。问：得几何？

答曰：为粟二十五斗九升。

此题显然是粟、粝两个量，我们已知用“份”为单位，粟5份，粝3份，题中又给粝米155升，用“升”为单位，于是易列出右率范。用四角阵原理得

粟 155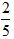×5÷3=259（升）

答：需要粟25斗9升。

例2：几何图形与分数问题。

如珠图：

珠矩形A 珠矩形B 珠矩形C

在上面的三个珠图中，不仅给出了一些量（如珠面积），而

且说明了用不同的单位去刻划量所得数的各种不同情况，如下表：

这样，把整数、真假带分数、比、约分、化简比，为何要做加减

乘除运算，为何产生各种应用问题，……，都联系起来融通一起了。

例如，（1）三个珠矩形A，B，C，其珠面积共是52珠，三者的

珠面积比是3: 4: 6，各有多少珠？（2）三个珠矩形A，B，C，三者的珠面积比是3: 4: 6，如果三珠矩形总的珠面积是S，那么，珠矩形A，B、C的珠面积各是多少？从而得到了代数式；再如，珠矩形B的珠面积比珠矩形C的珠面积少多少？就要进行式的运算，等等。

这些题目对中小学生来说，也算得上是比较难的。但如果运用率思想方法，只要看上面的率表，就可以做到一目了然。

实际上，本此精神，整个中小学数学内容（数、运算、式、方程、函数，几何图形……）都可以联系成一个整体，融通起来。

（三）率思想方法是用于构建《优因数学》的基因之一

《优因数学》就是把珠算符号、模型，率思想方法，符号化思想方法这三大优秀基因、范式融合起来，构建新的数学课程知识结构。“优因数学”的涵义再稍微具体一些，就是将中国传统数学之珠算符号、模型，及“率思想方法”与西方数学的符号化思想方法等中西方优秀数学基因、范式从基因层面上相融合，而构建的全新数学课程知识体系。通常提到“优因数学”，还包括：按照中西融合优秀数学基因、范式而构建的全新数学课程知识结构，并以《全日制义务教育数学课程标准》（实验稿）为底线，编写的《义务教育课程高标准实验数学教科书》，以及其教学实验。

率思想方法在构建《优因数学》的过程中起着设计师的作用。无论从认识数学，还是在运用数学，以及论证数学等诸方面，都涉及到率思想方法，都要运用率思想方法。整个初等数学教育的内容（包括启蒙阶段）可以用“率——函数”思想方法贯通起来。

（四）率思想方法在现代数学教育中的广泛应用

在认识数学方面：率思想方法改“人生学算糊涂始”为“人生学算明白始”。

（1）例如，伸出手问是几？学生一般都会立即答出：“5”。好像很正确，值得赞赏——其实，这是糊涂的。倘若以“手”为单位，就是“1”；以“双手”为单位，就是“”……学生学数学是从糊涂开始的。这样下去，当情况简单时，可以意会；但当情况复杂时，就会手足无措，不知如何是好了。

（2）再如，为什么算盘的一颗上珠表示5？——规定的，不讲道理，只有运用率思想方法才能说清楚道理。

在运用数学方面：上面说到解应用题，以及几何、分数等例题，就是率思想方法在数学运用方面能很好地起到简化作用的例子。实际上，现代学者之所以能发现率思想方法的巨大作用，就是从研究解决应用题的方法开始的，因此，运用率思想方法解决数学问题的独特作用是毫无疑问的。

在论证数学方面：由于率思想方法即“量-单位-数及其相互联系”的思想方法，是数学的最基本的功能单元，所以，要讲数学中的道理离不开这个基本的观念功能单元，时不时都要涉及到率。例如：古代如刘徽利用勾、股、弦“相与之势不失本率”的原理证明了勾股容方公式和勾股容圆公式。刘徽对勾股容方公式进行证明的原文：“幂图方在勾中，则方之两廉各自减小勾股，而其相与之势不失本率也。勾面之小勾股、股面之小勾股各并为中率。令股为中率，并勾、股为率，据见勾五步而今有之，得中方也。复令勾为中率，以并勾、股为率，据股十二步而今有之，则中方又可知。”

现代学者，根据率思想方法设计了率范（率表），给出了四角阵原理，因为它们处于数学的最基本部位，所以可以运用它们来论证基础数学的命题、法则和公式。

如，乘法对于代数和的分配律m×（a±b）= ma±mb，属于基本运算律，通常没法进行论证，一般都作为原理或公理处理，最多也就是举一些例子验证、说明以下即可。但如果运用率思想方法，就可以很简易地进行论证：

设L₁与L₂是两个同种量，用单位D₁量得的数分别是a和b；现再取一个单位用D₂表示（令D₁=mD₂）。求用D₂量得L₁与L₂的和的量与及差的量：

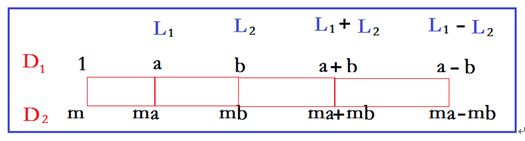
1先用四角阵原理求得L₁对应ma，L₂对应mb，按第二行求得L₁+L₂是ma+mb; L₁-L₂是ma-mb;（上表）

2先由第一行数求得L₁+L₂是a+b；L₁-L₂是a-b。再按四角阵原理，求得L₁+L₂对应m（a+b）; L₁-L₂对应m（a-b）。（上表）

L₁+L₂用D₂量只能是同一个数，所以ma+mb= m（a+b）

同理 ma-mb= m（a-b）
即 ma±mb= m（a±b）

再如，“分数的基本性质：分数的分子、分母同被一个不为0的数乘、除，分数的大小（值）不变。”通常，也是作原理，验证而已。但如果用率表和四角阵原理，可以进行论证：设量₁、量₂是同种两个量，

选用单位₂量得量₁为a，量得量₂为b；选单位₁、单位₃，与单位₂的对应如左表（m对1,1对k）再选量₁为单位（左表），用各单位刻划两个量，得到左率表。量₁刻划它本身，自然得1，再刻划量₂设得S，用一个单位量₁刻划一个量₂，只能得唯一的值，即S的值是唯一的。运用四角阵原理，由三个四角阵可得S的三个表达式：

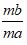S=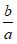， S=， S=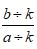

所以 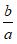== 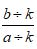（m≠0,k≠0）

这就清楚明白的说明了分数的基本性质。

率思想方法在现代数学教育中有着非常广泛的应用和巨大的简化作用，限于文章篇幅，本文只是进行了蜻蜓点水式的阐述。有兴趣的同行们，可以查看郭启庶教授所编写的有关著作和教材。

—————————————————

作者简介：刘芹英，女，理学博士，研究员。主要从事中国数学史和珠算史的研究。

参考文献

[1]郭书春主编，《中国古代数学典籍通汇》数学卷，卷一。

[2] 李继闵著，《九章算术》校正，陕西人们出版社，

[3] 郭书春著，《古代世界数学泰斗刘徽》，室内氡科学技术出版社，1992年3月第一版第一次印刷。

[4] 郭启庶著，《数学教学优因工程》，海南人民出版社，

[5] 郭启庶编著，《优因数学》教材。